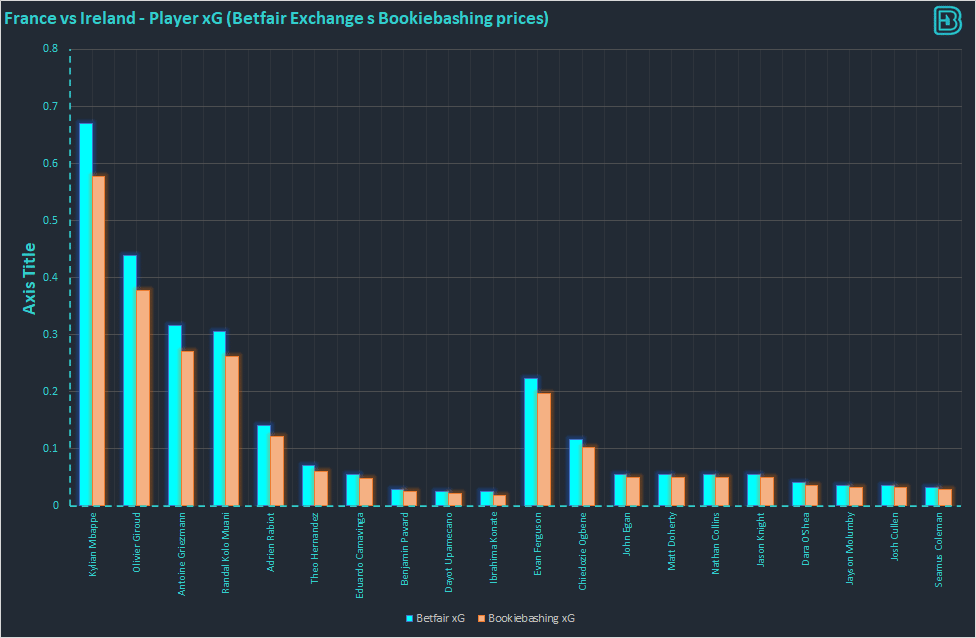
Every player in Ireland v France was trading 10-20% too low for AGS at kick off on the Exchanges last night. A layers dream.
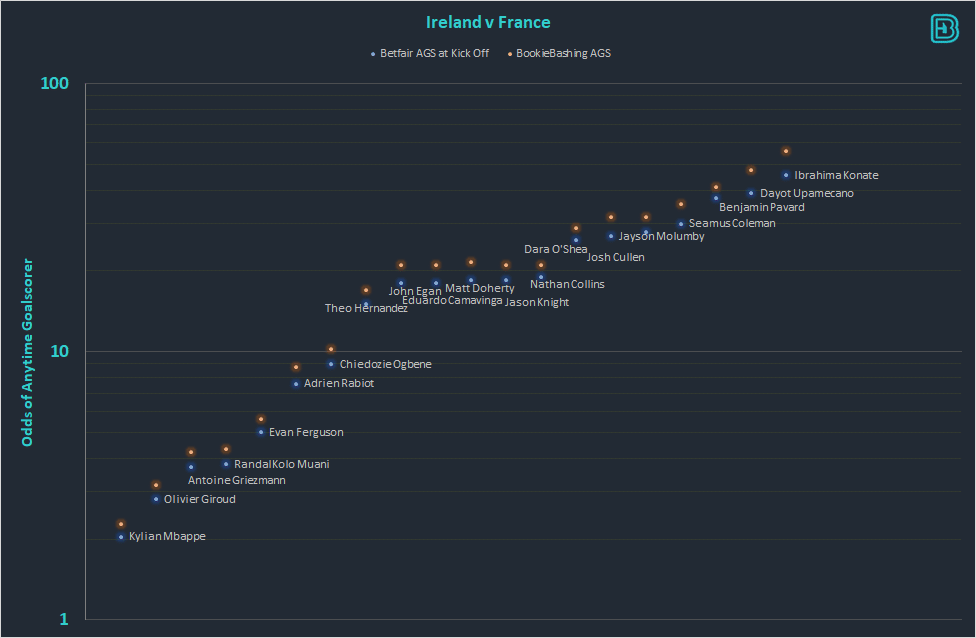
We can take all of the BFx AGS prices on the exchange at Kick Off (see table below). The fair prices were defined as “Last Price Matched, as long as it is between the current Back and Lay, else use the MidPoint”. The exchange was liquid and efficient on every player at Kick Off (unusually).
The AGS prices can be converted into xG using an inverse Poisson probability distribtion. From this xG, we can see that the Exchange predicted 2.077 xG from the starting XI of France, and 0.703 xG for Ireland. A total of 2.78 xG from both Starting XIs.
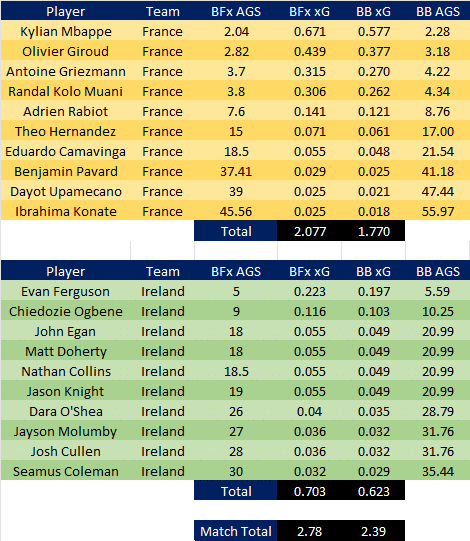
If the Exchange is efficient, this infers an xG of 2.78 for the Starting XIs. Data shows that 9% of goals are scored by SUBs (in games with 5 subs/team), which would equate to a match xG of 3.05.
*NB: Reality checking the playing time of subsititutes. 95 minutes were played in this match, and subs came on at 65, 77, 77, 77, 81, 86 and 92nd minutes. Substitutes played for 8.1% of this match.
A match xG of 3.05 from the AGS market on the exchanges was wildly optimistic. The market generally had a match xG of 2.63.
- The spreads had buy/sell lines of 2.55-2.75.
- Bet365 o/u for 2.5 was 1.95/1.9, suggesting fair odds around 2.03.
- The exchange was trading Over 2.5 at 2.02-2.04.
The bookie/exchange markets price of 2.03 for o2.5 goals suggests the Match xG was 2.62. Even if there were no substitutes predicted in this match, the AGS market on the exchange was optimistic. Adding in 9% of goals scored by substitutes suggests that the exchange market was optimistic by nearly half a goal. Laying all of the starting XI would have been a +EV strategy. The game finished 1-0. with a single goal for the right back Benjamin Pavard at 37.41 on the exchange.
This example shows the power at looking at the xG of players after team news has been arrived. We could only arrive at this conclusion at bookiebashing after looking at the xG of the players after team news, when we apply a process of normalisation to force the sum of the Starting XI to equal the Team xG (with Subs xG considered).